Creating a Vertex Displacement Shader
Tutorial
intermediate
+0XP
20 mins
48
Unity Technologies

In this tutorial, we will use Unity’s default render pipeline to create a shader that will deform and animate a flat mesh over time to simulate the motion of an ocean’s surface.
Languages available:
1. Creating a Vertex Displacement Shader
This tutorial has been verified using Unity 2019.4 LTS
In this tutorial, we will use Unity’s default render pipeline to create a shader that will deform and animate a flat mesh over time to simulate the motion of an ocean’s surface.

Real-time ocean simulations can be achieved via sine and cosine functions — their periodic ebb and flow have often been used to mimic the rise and fall of ocean waves without relying on complex wave functions (such as Fast Fourier Transforms). In this tutorial, we will refer to Jasper Flick’s guide for implementing a single Gerstner Wave, a modified sine function that can be used to create believable-looking waves in real-time.
2. Scene Setup
1. To begin, create a new plane by navigating to GameObject > 3D Object > Plane. Alternatively, you can create a plane with many subdivisions in Autodesk Maya or Max, then import that model into Unity. This is the best method for creating smoother waves.
2. Next, create a new Surface Shader by navigating to Assets > Create > Shader > Standard Surface Shader. Name it Waves and open the script.
3. We can extend the default Surface Shader to include a normal map (Figure 01) to allow our ocean surface to be affected by lighting.

Note how we first create a “bump” property for the normal map, then initialize it as a sampler2D. Next, we obtain its UV coordinates, then unpack the normals from the sampler2D so it can be assigned to the output fragment’s normals (Figure 02).
Shader "Custom/GerstnerWaves"
{
Properties
{
_MainTex (" Diffuse (RGB)", 2D) = "white" {}
_NormalMap ("Normal Map", 2D) = "bump" {}
}
SubShader
{
Tags { "RenderType"="Opaque" }
CGPROGRAM
#pragma surface surf Standard fullforwardshadows vertex:vert addshadow
sampler2D _MainTex;
sampler2D _NormalMap;
struct Input
{
float2 uv_MainTex;
float2 uv_NormalMap;
};
half _Glossiness;
half _Metallic;
fixed4 _Color;
// Add instancing support for this shader. You need to check 'Enable Instancing' on materials that use the shader.
// See https://docs.unity3d.com/Manual/GPUInstancing.html for more information about instancing.
// #pragma instancing_options assumeuniformscaling
UNITY_INSTANCING_BUFFER_START(Props)
// put more per-instance properties here
UNITY_INSTANCING_BUFFER_END(Props)
void vert(inout appdata_full v){
}
void surf (Input In, inout SurfaceOutputStandard o)
{
fixed4 c = tex2D (_MainTex, In.uv_MainTex) * _Tint;
o.Albedo = c.rgb;
o.Normal = UnpackNormal (tex2D (_NormalMap, IN.uv_NormalMap));
// Metallic and smoothness come from slider variables
o.Metallic = _Metallic;
o.Smoothness = _Glossiness;
o.Alpha = c.a;
}
ENDCG
}
FallBack "Diffuse"
}
Figure 02: This should be used as our starting template for the shader, merely setting up a standard appearance of our surface in the fragment shader.
3. Anatomy of a Sine Function
Our goal is to animate the vertices of our plane along a sine wave. First, though, we must define a displacement function that will be evaluated along the wave. Sine waves are periodic by nature and subsequently a good choice for modeling simplified ocean surface behavior.
Let’s look at some arbitrary value: X. A sine operation on X would be written like this in ShaderLab: sin(X).
From here, we clearly know that each value of X is being evaluated by sine. Behind the scenes, there is more happening. Let’s imagine now that X is the wavelength.
Implicitly, then, the full sine operation is affected by several other parameters:
_Amplitude * Sin( _Wavelength + _PhaseOffset)
Let’s explore how each of these parameters impacts the sine wave:
_Amplitude: This value defines the range of the wave along the y-axis. By default, the wave has a range of [-1, 1], meaning it will only go as high as 1 and as low as -1 along the y-axis.
_Wavelength: This is the length it takes for a wave to complete one cycle. The default is 2π, but it can be modified to create shorter or longer waves.
_PhaseOffset: This offset shifts the wave along the x-axis along some value. When this offset is combined with time, we are defining how fast the wave completes its cycle, otherwise known as its speed.
By default, _Amplitude and _Wavelength have a coefficient of 1 and _PhaseOffset has a value of 0 (meaning there is no change in the wave’s starting point). This is why, without modification, the above can be simplified to sin(X): 1 * (Sin(1 + 0) )= Sin(X)
With this overview, we are now ready to define the displacement function that will drive the primary movement of our ocean surface.
4. Setting up the Wave Displacement Function
Let’s extend the shader’s property block with the three properties that will drive the shape of our wave: direction, steepness, and frequency (Figure 03).
Properties
{
...
//Wave Properties
_Direction("Direction", Vector) = (1.0,0.0,0.0,1.0)
_Steepness ("Steepness", Range(0.1, 1.0)) = 0.5
_Freq ("Frequency", Range (1.0, 10.0)) = 1.0
}
Figure 03: These three properties will define the shape of our wave.
1. Above struct Input, create two float variables: one for steepness and one for frequency. Steepness will be used to modify the wave’s amplitude, while the frequency variable will be used to modify the wave’s period.
2. Next, create a float4 variable for direction. As the name implies, the direction variable will influence the direction the wave will travel and is best thought of as a stand-in for the direction of wind (if our ocean surface was affected by physical forces) (Figure 04).
//Wave Properties
float _Steepness, _Freq;
float4 _Direction;Figure 04: Defining the data types of each of these properties
Now we are going to begin completing our vert function.
3. Let’s begin by storing the position of each of the plane’s vertices as a float3 and normalizing the direction of the waves into a float4 (Figure 05).
//Wave displacement
//To begin, obtain the position of each vertex and normalize the wave direction
float3 pos = v.vertex.xyz;
float4 dir = normalize(_Direction);Figure 05: We must ensure that we normalize our direction vector, as it will make using it as a coefficient much easier later on.
4. Now, let’s define and store the default wavelength as 2π. Fortunately, Unity has a built-in variable for π, UNITY_PI (Figure 06).
//The full length of a sine wave is 2PI
float defaultWavelength = 2 * UNITY_PI;Figure 06: We simply multiply UNITY_PI by 2 to obtain the default wavelength of a sine wave.
5. Next, we will make the wavelength modifiable by dividing the default value of 2π by the frequency variable we created earlier. A larger frequency will create shorter, more frequent waves, and a smaller frequency will create longer, less frequent waves (Figure 07).
float wL = defaultWavelength / _Freq;Figure 07: If we want to modify the wavelength (wL), divide by desired frequency.
6. While our phase offset can be an ordinary integer, in real life, wave speed is determined by the square root of gravity divided by the wave’s length. As Unity does not have a built-in variable for the force of gravity, we can approximate it as 9.8 (m/s2) (Figure 08).
float phase = sqrt(9.8 / wL);Figure 08: Calculating the phase offset via gravity (9.8) divided by wavelength. Longer waves move faster.
With this data, we can create a generalized displacement function. This function is meant to accommodate an expanded version of sine (_Amplitude * Sin( _Wavelength + _PhaseOffset)). Please be aware that we have not yet defined our _Ampltitude, yet.
There are a couple things to note: We are taking the dot product of the position and direction, then multiplying that value by the original wavelength to obtain the final wavelength.
Additionally, we are subtracting the phase offset instead of adding it so the waves will move in the correct direction. This phase offset is multiplied by _Time.y to create the illusion of movement over time (_Time.y is a built-in shader property describing the amount of time passed since the Scene loaded) (Figure 09).
float disp = wL * (dot(dir, pos) - (phase * _Time.y));Figure 09: Defining our new displacement function
5. Steepness and Circular Displacement
The maximum amplitude, or peak, of a wave can be measured as the ratio between a wave’s steepness and its wavelength. Higher frequency waves will subsequently produce higher peaks. A greater steepness will amplify this effect.
1. Let’s express this ratio as a new float (Figure 10).
float peak = _Steepness/wL;Figure 10: The ratio between steepness and wavelength.
Next, we will evaluate our displacement function to displace the ocean vertices over time
Gerstner Waves are unique in that we see waves with sharper crests and longer, flatter valleys. These shapes require the plane to be displaced across all three axes. By extension, this displacement requires the vertices to move around in a circular pattern.
Let’s review the full sine operation again: _Amplitude * Sin( _Wavelength + _PhaseOffset).
We will substitute the following:
_Amplitude -> peak
_Wavelength + _PhaseOffset -> disp
The position of each vertex will be displaced via this operation along a circular path (recall the unit circle and how values along the x-axis were evaluated along cosine and values along the y-axis were evaluated on sine).
Note that each vertex along the x and z axes is constrained to its original position by simply adding the original position to the displaced position (Figure 11).
pos.x += dir.x * (peak * cos(disp));
pos.y = peak * sin(disp);
pos.z += dir.y * (peak * cos(disp));Figure 11: Updating the position of each vertex on the surface
Now we need to feed this back into the vertex data so our mesh can deform (Figure 12).
v.vertex.xyz = pos;Figure 12: Setting the vertex data
6. Loops
Try increasing the max range for the _Steepness value in the properties declaration to a larger number, such as 10. You will notice that the waves will begin to form loops.
The root of this problem goes back to partial derivatives. Let’s take a look at a simplified version of the displacement for x (without the directional coefficient and substituting in an arbitrary amplitude value (a) instead of using the peak ratio):
pos.x + (a * cos(x));If we were to take the derivative of this displacement, we would get:
1 - a * sin(x) * dx;In this setup, a large amplitude (or, in our case, a peak ratio in which the _Steepness value is too large) will cause the x-position of the displacement to be negative. In real life, a wave that moves backward will eventually break, crash, and disperse back onto the surface. However, as the Gerstner model does not account for these forces, the wave will move backwards indefinitely until it forms a loop. This is why our _Steepness value should be confined to the range [0, 1].
The figure below demonstrates the effect that high amplitudes have on the shape of Gerstner waves (Figure 13).
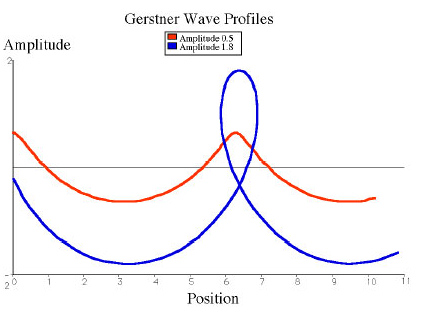
7. Setting the Material
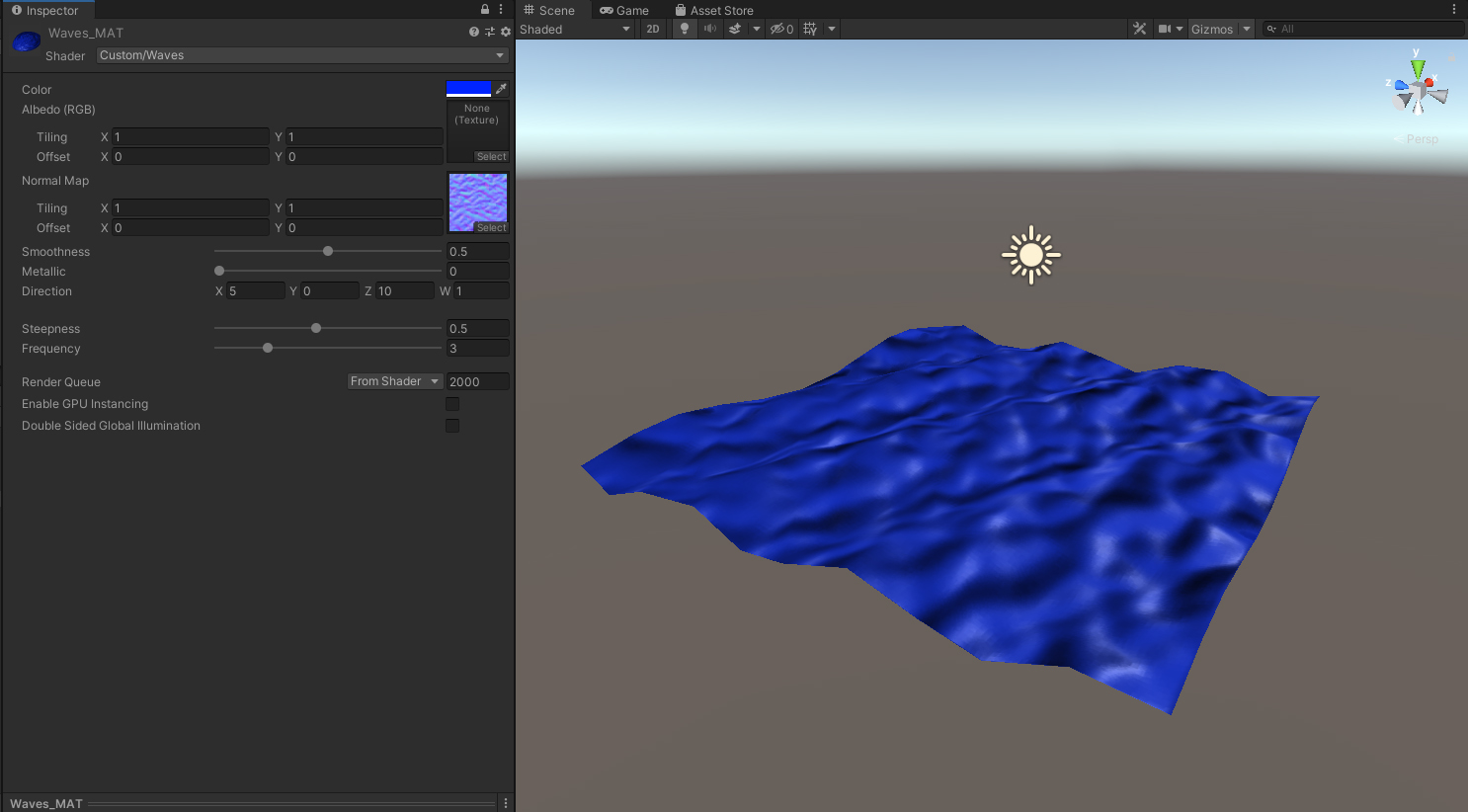
1. Create a new Material and name it Wave_Mat. Add it to your plane.
2. Set the shader on the Material to Custom/Waves and add your normal map to the Normal Map property.
3. Press Play and then make changes to the Direction, Steepness and Frequency properties until you’re satisfied with the look of the waves (Figure 14).
8. Conclusion
This serves as an introduction to displacing a mesh’s vertices via shaders. In essence, Gerstner waves are modified trigonometric waves that produce sharper peaks. We have learned how to modify this wave with a customizable amplitude, frequency, and wave direction. With this knowledge, we can now extend our wave shader to include multiple waves with varying frequencies and amplitudes. This will lend itself to a greater sense of realism without extensive modifications to the shader or runtime performance.